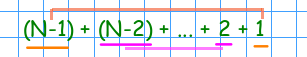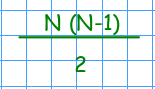Questo pagina è dedicata all'algoritmo di ordinamento per minimi successivi, detto anche selection sort.
Esso necessita di più scansioni: nella prima scansione, si cerca il minimo dell'intero vettore e lo si scambia con l'elemento in posizione 0.
Risorse collegate
Se vuoi approfondire la spiegazione dell'algoritmo guarda il video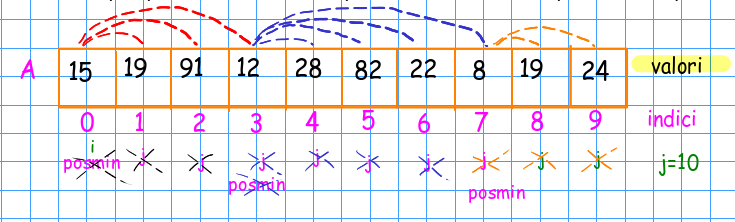 
Se ti interessa di più il video della codifica in linguaggio C 
Se vuoi scaricare il codice in linguaggio 
Se vuoi scaricare il codice in linguaggio 
Per il PDF di questo articolo 
Nella seconda scansione si prende in considerazione la porzione di vettore che va dalla posizione 1 in poi, si cerca il minimo in questa porzione e lo si scambia con l'elemento in posizione 1... e così per tutte le scansioni successive: se gli elementi del vettore sono N, saranno necessarie N-1 scansioni su porzioni di vettore via via più piccole.
Nella seconda scansione si prende in considerazione la Dunque, saranno necessarie due cicli iterativi annidati; il più esterno sarà controllato dall'indice i che punta alla cella candidata a contenere il minimo di ogni subvettore scandito: il minimo sarà indicato da un indice posmin inizializzato con il contenuto della variabile i e il cui valore cambierà ogniqualvolta si troverà, durante la scansione, un valore minore di quello puntato da posmin; il ciclo più interno sarà controllato dall'indice j che indicherà di volta in volta l'elemento da confrontare con l'elemento nella cella indicata da posmin.
Procedendo in questo modo alla fine il vettore risulterà ordinato.
La figura qui accanto tenta di mostrare quali sono i confronti effettuati e i valori assunti dalla variabile posmin durante la prima scansione. In questo esempio, dopo la prima scansione, l'elemento che si trova in posizione 7 (ultimo valore assunto da posmin) corrisponde al minimo del vettore e sarà scambiato di posto con l'elemento in posizione 0.
La figura qui accanto tenta di mostrare quali sono i confronti effettuati e i valori assunti dalla variabile posmin durante la prima scansione. In questo esempio, dopo la prima scansione, l'elemento che si trova in posizione 7 (ultimo valore assunto da posmin) corrisponde al minimo del vettore e sarà scambiato di posto con l'elemento in posizione 0.
Il numero di confronti effettuato sarà N-1 alla prima iterazione del ciclo più esterno, poi N-2 e così via a decrescere fino a 3, 2, 1.
Sommando il primo e l'ultimo addendo di questa serie si ottiene N, così come sommando il secondo e il penultimo addendo si ottiene ancora N. Questo sarà vero anche per tutti gli altri addendi equidistanti dagli estremi. Si può dimostrare che quella sommatoria è uguale a:
