Algoritmo Quicksort

In questo video ci si occupa dell'ordinamento dei dati in un vettore con l'algoritmo del quicksort.

Risorse collegate

Quicksort: codifica in linguaggio C

Quicksort: codifica in linguaggio Php

Analisi Quicksort su

Codifica Quicksort in linguaggio C su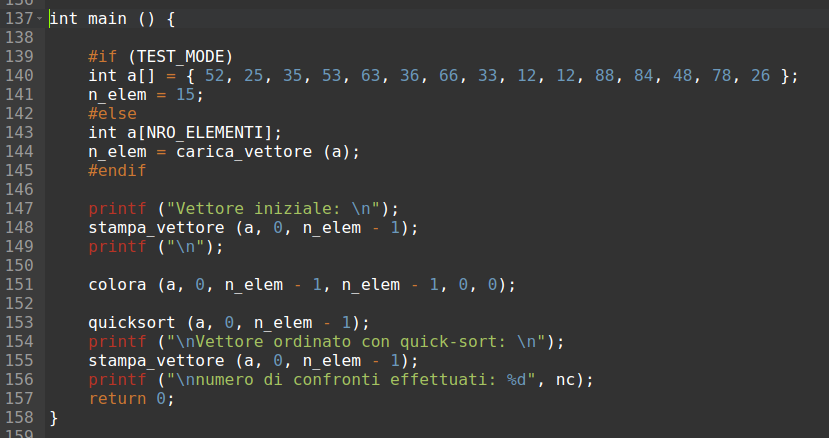

In questo video ci si occupa dell'ordinamento dei dati in un vettore con l'algoritmo del quicksort.

Esso è sicuramente tra gli algoritmi di ordinamento quello più efficiente; la sua strategia è la seguente: si sceglie un un elemento, in genere quello in prima posizione, che è chiamato perno o pivot e poi si partizione il vettore facendo in modo da mettere alla sinistra del perno tutti gli elementi più piccoli e alla sua destra tutti gli elementi più grandi. Il vettore iniziale viene diviso in due parti. Potremo così applicare la stessa strategia sia la parte di destra che alla parte di sinistra: procedendo nella maniera indicata otterrò porzioni sempre più piccole del vettore che alla fine si ridurranno a un solo elemento che risulterà ordinato, ponendo fine all'iterazione.

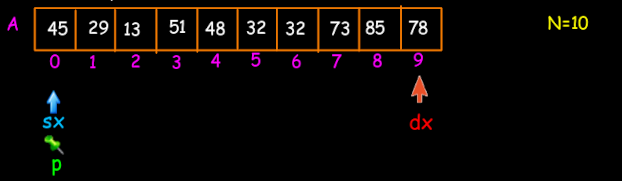
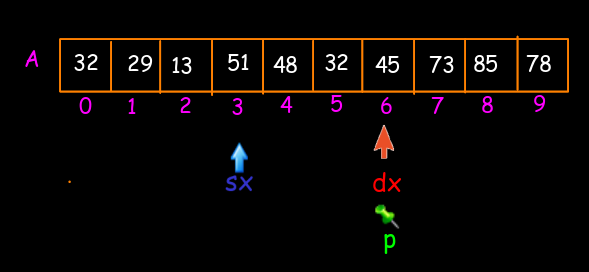
Supponiamo di avere il nostro vettore A che contiene 10 elementi memorizzati nelle posizioni che vanno da 0 a N-1. Avremo bisogno di 3 indici che chiameremo rispettivamente p (perno), sx (elemento di sinistra) e dx (elemento di destra). Inizialmente sx e p punteranno alla stessa posizione cioè alla posizione 0, mentre dx punterà alla posizione N-1. Si comincia col confrontare l'elemento puntato dal perno con l'elemento dx: se essi sono ordinati si lascia tutto inalterato, si decrementa l'indice dx e si ripete il ragionamento. Il codice C per far ciò è il seguente:

while (A[dx] >=A[p] && dx > sx) {dx--};

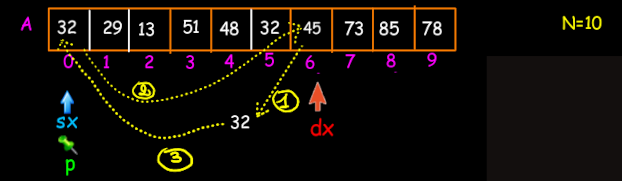
Arriverà il momento in cui dovrò effettuare uno scambio (in figura quando dx=6 e p=0, perché i rispettivi elementi puntati non sono in ordine); dopo lo scambio come ultima operazione sposterò il perno p su dx.

Poi si continua mettendo a confronto A[p] con A[sx]: se A[sx] <= A[p] sposteremo in avanti sx e ripeteremo il confronto.

while (A[sx] <=A[p] && sx < sx) {sx++};

Quando troveremo che A[sx] è maggiore di A[p], farò lo scambio e sposterò il perno su sx.

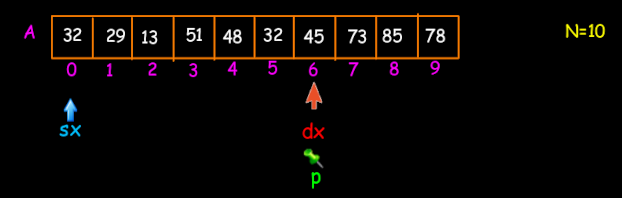
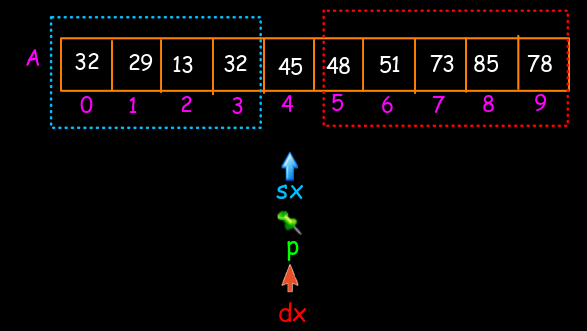
Procederemo così fino a quando sx, p e dx diventano uguali; quando ciò si verifica, il partizionamento è fatto poiché ho trovato la posizione corretta del perno. Se osserviamo i dati, noteremo che gli elementi che precedono il perno sono tutti minori di esso anche se non sono in ordine; mentre gli elementi che seguono il perno sono tutti più grandi del perno stesso, anche essi non ancora del tutto in ordine.

Ora non ci rimane altro da fare che ripetere il procedimento per i due sotto vettori che essendo più piccoli avranno bisogno di un numero minore di confronti. Il primo sotto-vettore sarà quello che va dalla posizione 0 alla posizione 3; mentre il secondo sotto-vettore sarà quello che va dalla posizione 5 alla posizione 9.

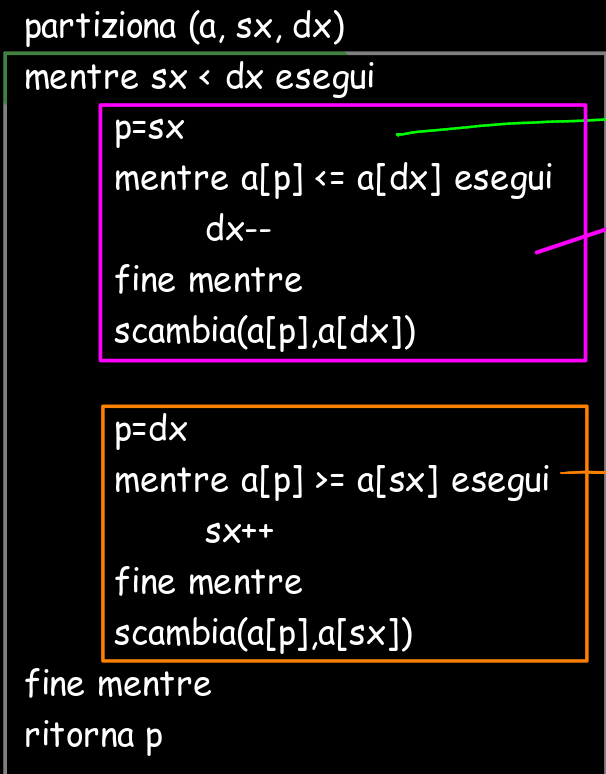
Delimitiamo la funzione di partizionamento: a questo scopo predisponiamo una funzione che prende in input il vettore A e gli indici sx e dx che puntano alla porzione di vettore da prendere in considerazione. La funzione restituirà un valore un valore p che punta alla posizione corretta del pivot prescelto di volta in volta.

Descriviamo come è fatta questa funzione al suo interno con la pseudo-codifica:

Incominciamo col fissare il perno su sx (p=sx) poi decrementiamo dx mentre a[p] è minore o uguale di a[dx]. Quando a[p] diventa maggiore di a[dx], scambiamo i due elementi.

Fissiamo il perno su dx (p=dx); incrementiamo sx mentre a[p] è maggiore o uguale di a[sx]. Quando a[p] diventa minore di a[sx], scambiamo i due elementi e ricominciamo.

Quando anche il ciclo esterno sarà concluso, avremo trovato la posizione corretta del perno e restituiamo la sua posizione al programma chiamante (return(p);)

Questa funzione sarà richiamata dalla funzione QuickSort, descritta di seguito.

La funzione quicksort() prende In input tre parametri:

• il vettore
• un indice che punta al primo elemento da considerare
• un indice Che punta all'ultimo elemento da considerare

In questo modo potremo prendere in considerazione porzioni sempre più piccole del vettore.

La funzione controlla prima se nel vettore ci sono almeno due elementi (primo<ultimo) e solo in questo caso richiama la funzione partiziona() di cui abbiamo già parlato facendosi restituire la posizione del perno; quindi richiama se stessa per applicare l'algoritmo del Quicksort alla porzione di sinistra e alla porzione di destra in cui è stato suddiviso il vettore iniziale dalla posizione del perno.

Nota 1 Questo è un esempio di funzione ricorsiva cioè una funzione che richiama se stessa. 

Nota 2 non confondere una direttiva con una variabile: una direttiva è rivolta al compilatore per istruirlo di sostituire ad ogni occorrenza di NRO_ELEMENTI il numero 100 e non occupa memoria.

se la condizione primo<ultimo è falsa la funzione esce immediatamente dall'ultimo livello di nesting della ricorsione ponendo così fine al processo. In altre parole la condizione primo<ultimo è fondamentale per evitare un loop infinito dell'algoritmo.

Il programma principale è molto semplice:

Ci sarà una prima fase di caricamento del vettore, poi esso sarà stampato prima dell'ordinamento, quindi si richiamerà la funzione Quicksort passando l'intero vettore come porzione da ordinare (a,0,n-1) e infine si stamperà nuovamente il contenuto del vettore dopo l'ordinamento