Scomposizione in fattori primi

Ci hanno insegnato alle scuole medie come si fa la scomposizione in fattori primi di un numero intero positivo.

Risorse collegate

clicca qui per vedere per vedere il flow chart

clicca qui per vedere per vedere la codifica in php

la spiegazione della codifica in php la trovi in questo articolo

clicca qui per vedere per vedere la codifica in linguaggio C e il relativo video

Adesso noi dobbiamo insegnarlo al computer. In questo articolo ci proponiamo di effettuare l'analisi necessaria per costruire il relativo programma. Costruiremo prima il flow Chart e poi lo tradurremo sia in linguaggio C ( e ) che in linguaggio PHP (vers. 1 ) e (vers. 2)

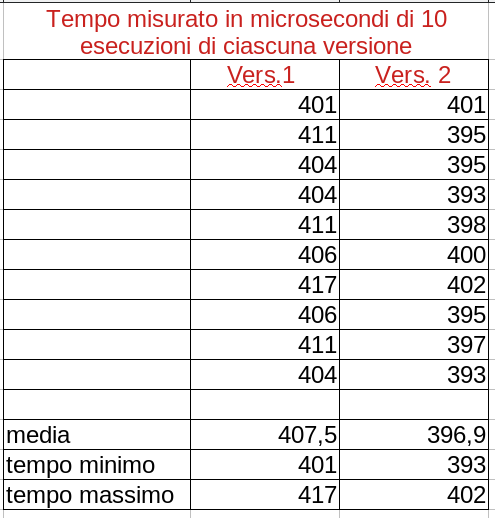
La versione 2 (articolo e/o ) è leggermente migliorativa rispetto alla versione 1 in quanto, dopo aver provato a dividere per 2, cerca i divisori solo fra i numeri dispari. Questo piccolo accorgimento migliora la velocità dell'algoritmo come si può notare dalla seguente tabella:

L'unico modo che abbiamo per cercare un divisore di un numero intero N con le conoscenze attuali e quello di andare per tentativi cioè provare prima a dividere per 2 poi a dividere per 3 poi a dividere per 5 e così via. Quindi già si intuisce che è necessario utilizzare una struttura iterativa. Il problema è adesso vedere da quale valore deve partire l'indice controlla questa struttura iterativa e fino a quale valore deve arrivare. Il valore iniziale sarà indubbiamente 2; il valore finale...beh ci dobbiamo pensare un po'.

La prima risposta che di solito viene data è "arriviamo fino a N", poi è facile convincerci che effettivamente basterebbe arrivare fino alla metà di N (perché non esistono divisori di N che siano maggiori di N/2); ma possiamo fare ancora meglio. Infatti vale la seguente

Osservazione: Se un numero N non è primo, allora esiste un suo divisore minore o uguale della radice quadrata di N (se non hai fede, clicca qui per la dimostrazione)

che significa? Significa che se arriviamo senza aver trovato un divisore di N, possiamo terminare la ricerca perché siamo certi che N è primo. Dunque, il valore finale sarà √N

La pseudocodifica della struttura iterativa sarà:

 
k=2
mentre(k <= √N){
         ...
         k=k + 1 
 } 

dove k è un indice candidato divisore di N.

Dobbiamo verificare se k è effettivamente un divisore di N. A tal scopo calcoliamo il resto della divisione (funzione modulo!) fra n e k. Se il resto è zero allora k è un divisore di N

k=2
mentre(k <= √N){
     resto= N modulo k
    ...
    k=k + 1
}

C'è una piccola complicazione. Non ci basta sapere se k è un divisore di N ma vogliamo sapere quante volte k divide N. Facciamo un esempio:

se N=80 la sua scomposizione é 2⁴ * 5 perciò 2 divide 80 quattro volte. Perciò abbiamo bisogno di un contatore che chiameremo exp (valore iniziale 0) e di una ulteriore struttura iterativa che calcoli quante volte k divide N.

k=2
mentre(k <= √N){
    resto = N modulo k
    exp=0
    mentre (resto=0){ 
        exp=exp+1
        N=N/k
        resto=N modulo k // calcoliamo il NUOVO n modulo k ( N è stato modificato)
    }
...
k=k + 1
}
 

Quando usciamo dal ciclo suddetto exp conterrà il valore dell'esponente che però potrà essere anche uguale a zero. Non ci resta altro che visualizzare il valore del divisore k e di exp, ma solo se exp è diverso da zero. Quando usciamo dal ciclo più esterno se N è diverso da 1, lo mostriamo perché è l'ultimo fattore della scomposizione.

k=2
mentre(k <= √N){
    resto = N modulo k
    exp=0
    mentre (resto=0){ 
        exp=exp+1 //incrementiamo il contatore dell'esponente
        N=N/k
        resto=N modulo k // calcoliamo il NUOVO n modulo k ( N è stato modificato)
    }
    Se (exp<>0) allora
         output divisore ^ exp
    fine se
    k=k + 1
}
Se (N<>1) allora
     output N
fine se

NOTA: la condizione k <= √N è interessante perché ad ogni ciclo sia k che √N sono ricalcolati, consentendo all'algoritmo di terminare il proprio compito più velocemente. l'algoritmo cioè diventa estremamente efficiente. Infatti se p.e. N=1680

quando la condizione viene testata la prima volta k=2, N=1680 e √N = 40.98

quando la condizione viene testata la seconda volta k=3, N=105 e √N = 10.24

e così via. Perciò si può notare che l'insieme dei valori da testare per scoprire i divisori viene ridotto drasticamente ad ogni ciclo esterno.